Prerequisites

The following sections describe the prerequisites for using MPSKit. If you are already familiar with the concepts of MPSKit and TensorKit, you can skip to the Overview section.

TensorKit

using TensorKit

MPSKit uses the tensors defined in TensorKit.jl as its underlying data structure. This is what allows the library to be generic with respect to the symmetry of the tensors. The main difference with regular multi-dimensional arrays is the notion of a partition of the dimensions in incoming and outgoing, which are respectively called domain and codomain. In other words, a TensorMap can be interpreted as a linear map from its domain to its codomain. Additionally, as generic symmetries are supported, in general the structure of the indices are not just integers, but are given by spaces.

The general syntax for creating a tensor is one of the following equivalent forms:

TensorMap(initializer, scalartype, codomain, domain)
TensorMap(initializer, scalartype, codomain ← domain) # ← is the `\leftarrow` operator

For example, the following creates a random tensor with three legs, each of which has dimension two, however with different partitions.

V1 = ℂ^2 # ℂ is the `\bbC` operator, equivalent to ComplexSpace(10)
t1 = Tensor(rand, Float64, V1 ⊗ V1 ⊗ V1) # all spaces in codomain
t2 = TensorMap(rand, Float64, V1, V1 ⊗ V1) # one space in codomain, two in domain

try
    t1 + t2 # incompatible partition
catch err
    println(err)
end

try
    t1 + permute(t2, (1, 2, 3), ()) # incompatible arrows
catch err
    println(err)
end

SpaceMismatch("(ℂ^2 ⊗ ℂ^2 ⊗ ℂ^2) ← ProductSpace{TensorKit.ComplexSpace, 0}() ≠ ℂ^2 ← (ℂ^2 ⊗ ℂ^2)")
SpaceMismatch("(ℂ^2 ⊗ ℂ^2 ⊗ ℂ^2) ← ProductSpace{TensorKit.ComplexSpace, 0}() ≠ (ℂ^2 ⊗ (ℂ^2)' ⊗ (ℂ^2)') ← ProductSpace{TensorKit.ComplexSpace, 0}()")

These abstract objects can represent not only plain arrays but also symmetric tensors. The following creates a symmetric tensor with ℤ₂ symmetry, again with three legs of dimension two. However, now the dimension two is now split over even and odd sectors of ℤ₂.

V2 = Z2Space(0 => 1, 1 => 1)
t3 = TensorMap(rand, Float64, V2 ⊗ V2, V2)

TensorMap((Rep[ℤ₂](0=>1, 1=>1) ⊗ Rep[ℤ₂](0=>1, 1=>1)) ← Rep[ℤ₂](0=>1, 1=>1)):
* Data for sector (Irrep[ℤ₂](0), Irrep[ℤ₂](0)) ← (Irrep[ℤ₂](0),):
[:, :, 1] =
 0.5799062942772701
* Data for sector (Irrep[ℤ₂](1), Irrep[ℤ₂](1)) ← (Irrep[ℤ₂](0),):
[:, :, 1] =
 0.034655024404386614
* Data for sector (Irrep[ℤ₂](1), Irrep[ℤ₂](0)) ← (Irrep[ℤ₂](1),):
[:, :, 1] =
 0.8968666139925996
* Data for sector (Irrep[ℤ₂](0), Irrep[ℤ₂](1)) ← (Irrep[ℤ₂](1),):
[:, :, 1] =
 0.6739101131398383

For more information, check out the TensorKit documentation!

Conventions

The general definition of an MPS tensor is as follows:

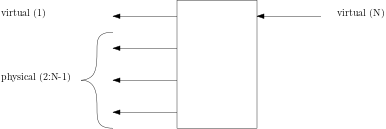
These tensors are allowed to have an arbitrary number of physical legs, and both FiniteMPS as well as InfiniteMPS will be able to handle the resulting objects. This allows for example for the definition of boundary tensors in PEPS code, which have two physical legs.

Similarly, the definition of a bond tensor, appearing in between two MPS tensors, is as follows:

Finally, the definition of a MPO tensor, which is used to represent statistical mechanics problems as well as quantum hamiltonians, is represented as:

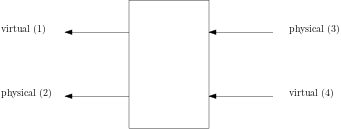
While this results at first glance in the not very intuitive ordering of spaces as $V_l \otimes P \leftarrow P \otimes V_r$, this is actually the most natural ordering for keeping the algorithms planar. In particular, this is relevant for dealing with fermionic systems, where additional crossings would lead to sign problems.